Use SMT Solvers to generate crossword grids (3)

13 November 2019

development z3

This post is part of a series on using SMT Solvers to generate crossword grids.

• Introduction to SMT, and programming with SMT Solvers;
• Definitions and first formulas;
• Plumbing everything together, complete formula, and results (currently reading).

Thanks @geistindersh for his feedback, and corrections!

In the two previous posts, we covered how to represent:

• Valid words;
• The potential values they can have, taking their length into consideration;
• And their “crossing points”, i.e., the characters some of them must have in common.

We presented how the formulas derived from these representations are fed into a Solver, that would lead us to a set of values that we then “mapped back” into the grid to have it completed.

Although the savant part of the job is done, a couple of points that are left to discuss to end the series:

• Automate the formula generation, from potentially different grid frames;
• Present measurements we made and results we had;
• Cry over the lack of efficiency Discuss some potential improvements.

Formula generation

In the previous post, we presented how to write formulas to encode crossword grids constraints.

So far, the process has been very manual: declaring a variable for each word, and explicitly adding the “intersection” constraint. One can easily see how this can become arduous as we will want to generate bigger grids.

Ambitiously, our ultimate goal is to be able to generate a grid such as this real world one, which dimension is 17x12, counts 64 words and 162 intersections in total.

Because we interact with Z3 using its Python API, it makes it easy for us to write a program in this language to do all the fancy plumbing we need to:

• Create the variables from a grid frame;
• Formulate the constraints using these variables: values words can take, and the common letters they must respect on intersections;
• Deal with a large wordlist: 200 000+ words.

Variables

Unlike in the previous post, where we had to deal with a small number of words to represent, we expect here to deal with a consequent number of variables.

Naming them \(\text{horizontal}\), or \(\text{vertical}\) would be very limiting; Still, using a naming scheme to help us locate words in the grid from the name of the variable use to represent them is an helpful idea.

Hence, let’s arbitrarily decide that our variable names will follow the pattern: \(direction\_x\_y\), where \(x\) and \(y\) are respectively the line and column components of the coordinate of the first letter of the word, and \(direction\) takes the value h or v if the word is either horizontal or vertical. We count coordinates respecting the French reading direction. So, the top left corner has coordinates \((0, 0)\).

Here is an example of a portion of a grid:

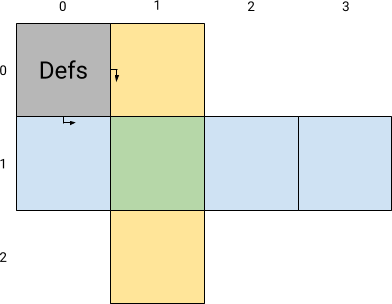
• \(h\_1\_0\) represents the horizontal word which first letter is on the cell \((1, 0)\), in light blue;
• \(v\_0\_1\) represents the vertical word which first letter is on the cell \((0, 1)\), in light orange.

Grid

The biggest grid we are aiming to represent counts 64 words to determine. Hence, we need to create the same number of variables, respecting the naming convention we just presented.

Doing so manually would be time consuming, especially if we expect to represent different grid frames (I did). So, I wrote a Python program to generate the variables out of a grid represented as an array of 0s and 1s, as shown in the following picture:

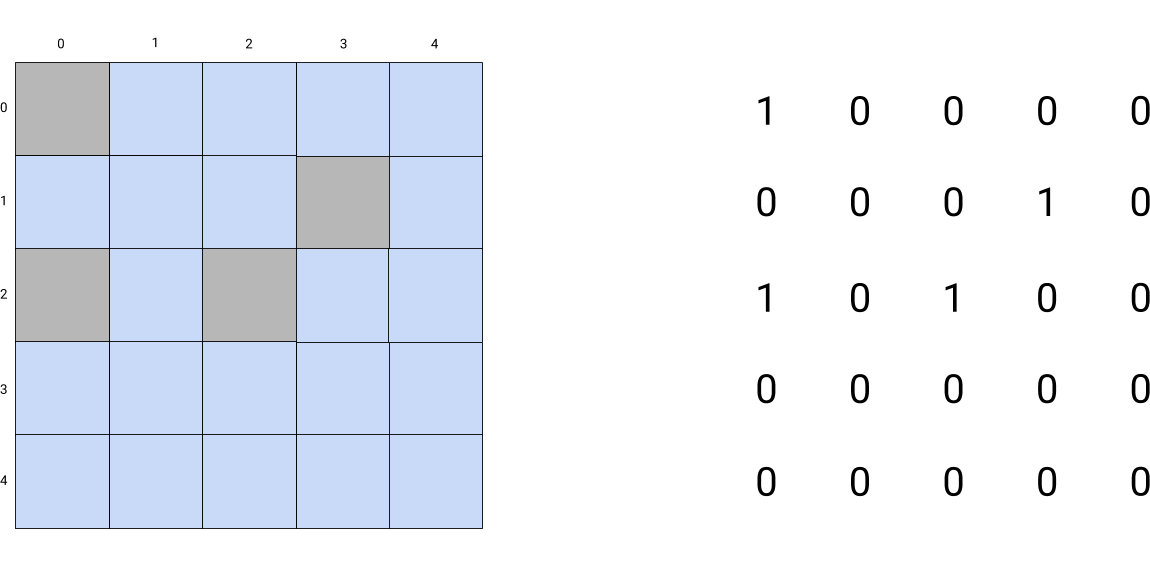
From this representation, a complete formula can be generated (the different variables, with the values they can take, and the intersection constraints).

Stop waving your hands. Where is the code?

The complete code is available in a GitHub repository, and too long to completely expose here. Don’t let the amount of files intimidate you, the principles exposed in this series are the one implemented. Let’s briefly present its content:

• francais.txt: The wordlist where the words are chosen from;
• generate_dictionary.py: A script to generate this “normalised” wordlist (remove diacritics, deduplicate) out of a French wordlist found online;
• dictionary.py: The representation of the wordlist as a Python structure, with the logic of “splitting” it into several pieces per the word size (as detailed in the previous post).
• grid.py: The scanning of a grid from 0s and 1s, and interface to query grid related content, such as: list of words and intersections, with their coordinates, following the convention exposed above.
• test_grid.py: Some unit test for the above logic;
• solve.py: The central piece, making use of the above components to generate the formula as exposed in this series, call the solver, and print a solution ( when  if found).

Results

I ran the solve.py program on a Lenovo x220, with an Intel Core i5-2520M CPU (dual core, 2.50GHz base frequency), and 8GB of RAM, running on NixOS 20.03 ¹. I used different parameters, varying the size of the grid and wordlists, at first to ensure that it worked as expected and produced valid solutions, then to measure its efficiency.

The wordlists’ sized has been reduced by shuffling the original (to keep a certain diversity among the options), then selecting only the first elements from it. I took three different grid sizes: small, medium, and large (respectively 6x3, 12x6, and 17x12); With the two smallest truncated from the original 17x12 frame.

Here are the results obtained with our solution, implemented with the code presented earlier:

• On a 6x3 grid, with wordlists each reduced to 200 words, SAT with a solution, in ~6 seconds;
• On a 6x3 grid, with complete wordlists, SAT with a solution, in ~1.5 hours;
• On a 12x6 grid, with wordlists each reduced to 200 words, UNSAT, in ~5 minutes;
• On a 12x6 grid, with wordlists each reduced to 500 words, UNSAT, in ~6 hours;
• On a 12x6 grid, with complete wordlists, Unknown, timed out after ~100 hours;
•  On a 17x12 grid, with complete wordlists …

Generation is working fairly quickly on small grids, using a reduced number of words to pick from. However, although the production of the formula increases linearly (in the size of the grid, and number of words per wordlists), the time it takes for the Solver to solve a given query grows at least quadratically (if not exponentially).

In the end, I did not get the patience to run the experiment for the targeted 17x12 grid.

Improvements

During the development of this idea, the evolution of the code to support it, and the writing of this series, some points of interest regarding future improvements arose.

First, we point out that the support for String theory is very recent in Z3. Maybe our results could be improved by using a Solver with a more efficient support it. With the same objective, it could be interesting to have a look at Z3’s internals, and get a better understanding of the practical limitations of using it in our context.

Second, I started wondering if one could come up with efficient strategies to reduce the size of the queries without losing too much accuracy, for example:

• Take guesses for words coming from lists containing a lot of words;
• Clean the wordlists from words that are containing letters with low occurrences in the dictionary. For example, isolated words (farther from the others), defined using the Levenshtein distance;
• “Divide and conquer”: isolate portions of the grid that could be solved separately, adapting the wordlists accordingly. For example solving the bottom right corner using wordlists of truncated words, where only their “end” portion is left. This approach would reduce the size of the wordlist too, as verbs with the same “ending” in their conjugation would be mapped to a single entry in the truncated wordlist.

Last words

All in all, using Solver to generate crossword grids is not the most efficient way to do it, making its use impractical: I will never be able to start my crossword editor startup…

However, this idea allowed us to explore several concepts around the use of SMT Solvers, to help us find solution to algorithmic problems.

In particular, we discussed in details how we can model (encode) crossword grids, to get a program give us, although very slowly, valid solutions!

Hope you found this journey very cool; At least it was from my side.